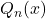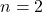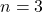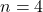Partie I – un exemple
Soit ![]()
![]()
- Le nombre 2 est-il racine du polynôme
P? - Trouver trois nombres réels
a,betctels que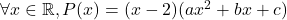
- Déterminer le signe de
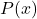
- Factoriser
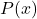
Partie II – un autre exemple et une généralité
Soit ![]()
![]()
- Trouver une racine évidente du polynôme
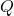
- Factoriser
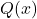
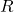
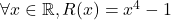
- Factoriser si possible
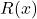
- Conjecturer sur la factorisation de
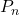
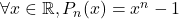
- Démontrer cette conjecture.
Partie III – Une autre généralité
Soit ![]()
![]()
![]()
- Trouver une racine évidente du polynôme
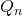
- Factoriser