Soit un triangle ![]()
On pose ![]()
![]()
![]()
On appelle ![]()
![]()
![]()
![]()
On veut démontrer que ![]()
I. Cas où le triangle 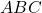
Un triangle acutangle est un triangle dont tous les angles sont aigus.
Soit H le pied de la hauteur du triangle ![]()
![]()
- Faire une figure.
- Exprimer la longueur
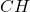

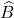
- Exprimer la longueur
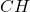
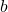
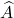
- En déduire la relation
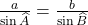
- De la même façon, démontrer que
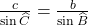
- a. Exprimer
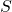


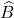
b. En déduire que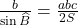
- Soit
Dle point diamétralement opposé au point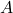
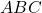
a. Exprimer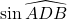

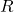
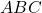
b. Que dire des angles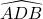
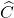
c. En déduire que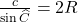
- Conclure.
II. Cas où le triangle 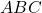
Un triangle obtusangle est un triangle qui possède un angle obtus.
Considérons dans notre cas que l’angle ![]()
Le but est de répondre aux même questions que dans la partie I. Cependant, les questions 2, 3, 4, 6a et 6b auront des réponses identiques donc il sera inutile de les traiter.
III. Cas où le triangle 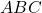
Considérons dans notre cas que le triangle est rectangle en ![]()
Le but est de répondre aux même questions que dans la partie I. Cependant, les questions 2, 3, 4, 6a et 6b auront des réponses identiques donc il sera inutile de les traiter. De plus, on change la question 7 par:
a. Exprimer
en fonction de.
b. En déduire que.