Activité XVII – Variable aléatoire

Le temps d’attente (en minutes) à l’arrêt d’un bus peut-être modélisé par une variable aléatoire $T$ donc la loi de probabilité est donnée ci-dessous.

$t_i$	$1$	$2$	$3$	$4$	$5$	$6$
$\mathbb{P}\left(T=t_i\right)$	$0,28$	$0,22$	$0,19$	$0,16$	$0,10$	$0,05$

Dans un premier temps, nous allons écrire les données du problème dans Thonny et importer les bibliothèques nécessaires à cette activité:

from math import sqrt
from random import random
temps_attente=[1, 2, 3, 4, 5, 6]
proba=[0.28, 0.22, 0.19, 0.16, 0.10, 0.05]

I. Simulation de l’attente

Compléter la fonction suivante, qui simule le jeu ci-dessus.

def attente():
    nbAleatoire=random()
    if nbAleatoire<=0.28:
        temps=1
    elif nbAleatoire<=0.50:
        temps=2
    elif nbAleatoire<=...:
        temps=3
    elif nbAleatoire<=...:
        temps=4
    elif nbAleatoire<=...:
        temps=5
    else:
        temps=6
    return ...

Implémenter la fonction dans le logiciel Thonny.

II. Simulation de n expériences

Le but est de créer une liste correspondant à un échantillon des temps d’attente à l’arrêt du bus.

Créer une fonction echantillon() ayant pour paramètre $n$ , la taille de l’échantillon et qui retourne la liste des $n$ attentes à l’arrêt du bus.

III. Convergence de la moyenne

Que font les fonctions suivantes:

def somme(liste):
    resultat=0
    for elt in liste:
        resultat = resultat + elt
    return resultat

def moyenne(liste):
    return somme(liste)/len(liste)

Tester la fonction moyenne sur des échantillons de taille de plus en plus grande. Que remarquez-vous?

III. Espérance

Créer la fonction esperance() ayant pour paramètres 2 listes valeurs et probabilites, et qui retourne l’espérence de la variable aléatoire dont la loi est donnée par les deux listes.
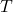
Quelle est l’espérance de la varaible aléatoire ? On écrira dans le shell:
```
>>> esperance(temps_attente, proba)
```
Calculer, pour plusieurs valeurs de , l’écart entre la moyenne d’un échantillon de taille et l’espérance. On écrira dans le shell, par exemple:
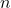
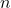
```
>>> moyenne(echantillon(10))-esperance(temps_attente, proba)
```
Que remarquez-vous?
Quelle conjecture peut-on faire que l’espérance par rapport à la moyenne d’un échantillon?

IV. Variance et ecart type

Créer la fonction variance() ayant pour paramètres 2 listes valeurs et probabilites, et qui retourne la variance de la variable aléatoire dont la loi est donnée par les deux listes.
Créer la fonction ecart_type() ayant pour paramètres 2 listes valeurs et probabilites, et qui retourne l’écart type de la variable aléatoire dont la loi est donnée par les deux listes.

V. Calcul d’une proportion

On considère $N$ échantillons de taille $n$ . Si on appelle $\mu$ l’espérance de la loi de la variable aléatoire $T$ et $\sigma$ son écart type, écrire une fonction simulation() ayant pour paramètres:

$N$ , le nombre d’échantillons à simuler.
$n$ , la taille de chaque échantillon.
$valeurs$ , les valeurs prises par la variable aléatoire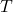 $T$ .
$probabilites$ , les probabilités correspondant aux valeurs ci-dessus.

Cette fonction devra retourner la proportion d’échantillons ayant une moyenne de temps d’attente comprise entre $\mu - \frac{2\sigma}{\sqrt{n}}$ et $\mu + \frac{2\sigma}{\sqrt{n}}$ .

Tester plusieurs fois cette fonction. Que remarquez-vous?