I – La suite de Syracuse
Soit ![]()
La suite de Syracuse du nombre ![]()
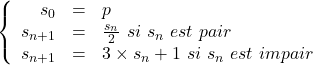
- Choisir un nombre
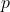
- En python, l’opérateur
%renvoie le reste de la division euclidienne.
Ainsi72 % 5renvoie le reste de la division euclidienne de 72 par 5 soit 2:>>> 72 % 5 2Que renvoient les commandes suivantes?
>>> 17 % 2 >>> 35 % 2 >>> 26 % 2 >>> 1354 % 2 - Soit
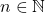
Que peut-on dire de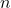
n % 2renvoie 1?
Que peut-on dire de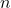
n % 2renvoie 0? - En Python, créer une fonction
Syracuse()de paramètresnetp, qui renvoie le terme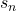
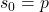
- Tester la fonction
Syracuse(). Par exemple:>>> Syracuse(15,5) 106 - Créer une fonction
liste_syracuse()de paramètresnbetp, et qui retourne la liste desnbpremiers termes de la suite de Syracuse du nombre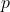
Par exemple:>>> liste_syracuse(6, 12) [12, 6, 3, 10, 5, 16] - Que remarquez-vous lorsque
nbest grand? - Quel conjecture pouvez-vous faire sur la suite de Syracuse d’un nombre
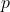 ?
? - Créer une fonction
liste_syracuse2()de paramètre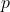
1.
II – La suite de Fibonnacci
La suite de Fibonnacci est définie de la façon suivante:
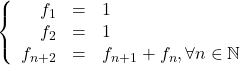
- Calculer les 5 premiers termes de la suite
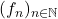
- En Python, créer une fonction
Fibonnacci()de paramètren, qui retourne le terme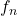
- Vérifier le bon fonctionnement de votre fonction grâce aux 5 premiers termes de la suite de Fibonacci.
- Créer une fonction
liste_fibonnacci()de paramètrenbqui retourne la liste desnbpremiers termes de la suite de Fibonacci.>>> liste_fibonnacci(6) [1, 1, 2, 3, 5, 8]