I. Médianes d’un triangle
- Tracer une triangle
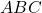
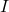
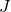
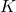
![Rendered by QuickLaTeX.com [BC]](https://courscaneri.ovh/wp-content/ql-cache/quicklatex.com-9387d62be762bd9ef56e825286f4f76f_l3.png)
![Rendered by QuickLaTeX.com [AC]](https://courscaneri.ovh/wp-content/ql-cache/quicklatex.com-0a0e57b19e7556df3cf40e3dd363fe1a_l3.png)
![Rendered by QuickLaTeX.com [AB]](https://courscaneri.ovh/wp-content/ql-cache/quicklatex.com-3eeb420b9fe46d9d1ef0ace9ca142a1f_l3.png)
- Tracer les trois médianes de ce triangle.
- Que dire des trois médianes?
- Nous allons démontrer la conjecture.
Soit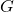
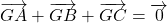
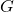
a. Démontrer que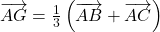
b. En déduire que le point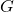
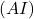
c. Démontrer de la même façon que le point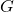
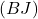
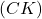
d. Conclure. - Soit
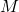
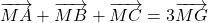
II. Droite d’Euler d’un triangle
Soit un triangle ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
- Soit
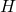
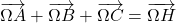
a. Démontrer que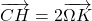
b. Calculer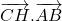
c. Que représente la droite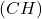
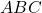
d. De même, que représentent les droites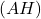
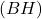
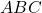
e. Que dire des trois hauteurs d’un triangle?Le point
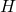
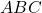
- Démontrer que les points
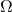
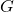
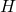
La droite qui passe par le centre de gravité, l’orthocentre et le centre du cercle circonscrit à un triangle s’appelle la droite d’Euler.