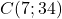Activité XVIII – Problèmes – Cours de M. Caneri

Problème 1

Le capitaine d’un bateau de tourisme veut montrer le littoral à ses passagers. Cependant, un rocher est à 200m de la côte. Il choisit donc de se placer toujours à équidistance du rocher et de la côte.

Pour modéliser le problème, on se placera dans un repère orthonormé $\left(O;\overrightarrow{i},\overrightarrow{j}\right)$ .
Le rocher est représenté par le point $R(0;2)$ et le bateau par le point $B(x;y)$ .
La côte est représentée par l’axe des abscisses.

Déterminer l’expression de la distance entre le rocher et le bateau en fonction de $x$ et $y$ .
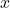
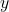
Déterminer l’expression de la distance entre le bateau et la côte en fonction de $x$ et $y$ .
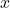
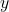
En déduire l’équation réduite de l’ensemble des points représentant la trajectoire du bâteau.
Quel est le nom de cette trajectoire?
Un homme, qui se trouve à l’est du rocher, nage en direction du nord en partant de la côte à 250 mètre du rocher. Il est représenté par le point $H(a;y)$ avec $a$ fixé et $y$ variable.
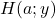
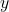
a. Quelle est la valeur de $a$ ?
b. A quelle distance de la côte atteindra-t-il la trajectoire du bateau?
Une femme nage en direction de l’est en partant du rocher.
Elle est représentée par le point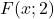 $F(x;2)$ .
A quelle distance du rocher atteindra-t-elle la trajectoire du bateau?

Problème 2

Dans un repère orthonormé $\left(O;\overrightarrow{i},\overrightarrow{j}\right)$ , on considère le cercle de centre $A(3;19)$ et de rayon 15.

Déterminer, si elles existent les coordonnées des points d’intersection de ce cercle et de la droite parallèle à l’axe des ordonnées passant par le point $B(12;5)$ .
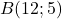
Déterminer, si elles existent les coordonnées des points d’intersection de ce cercle et de la droite parallèle à l’axe des abscisses passant par le point $C(7;34)$ .