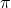Le but de cette activité est de donner une approximation de la valeur de ![]()
Partie I – Préliminaires
- Soit
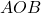
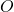
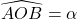
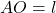
Déterminer la longueur du côté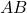
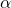
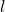
- Soit
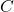
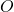
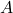
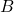
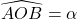
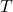
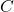
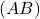
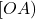
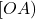
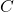
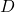
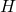 le pied de la hauteur du triangle
le pied de la hauteur du triangle 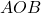
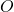
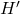
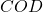
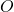
- Faire une figure.
- Calculer en fonction de
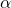
- la longueur
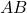
- la longueur
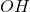
- la longueur
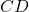
- la longueur
Partie II – Approximation de 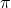
Soit ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
La figure ci-dessous représente le cas où ![]()
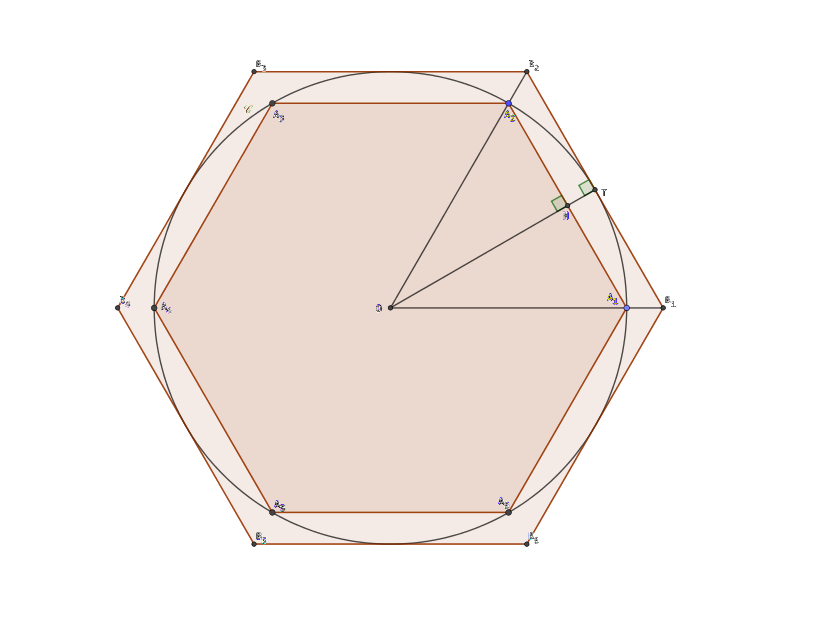
- On pose
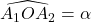
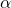
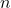
- En déduire la longueur
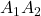
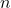
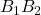
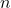
- Déterminer le périmètre
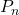
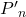
- Justifier le fait que
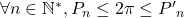
- Calculer
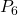
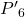
- Nous allons trouver une approximation de
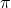
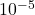
- Exécuter le logiciel Thonny.
- Ecrire en ligne 1:
from math import sin, cos, tan, radians,pow - Créer une fonction
perimetre_interieur()ayant pour paramètren, le nombre de côtés du polygône intérieur. - Créer un fonction
perimetre_exterieur()ayant pour paramètren, le nombre de côtés du polygône extérieur. - Créer un fonction
archimede()qui prend un nombreerreuren paramètre qui correspond à l’erreur commise par l’approximation et qui retourne lapproximation du nombre