Activité XVI – Variables aléatoires

I. Formules de König-Huygens

On considère une loi de probabilité définie sur un univers $\Omega$ et $X$ une variable aléatoire définie sur $\Omega$ dont la loi de probabilité est résumée dans le tableau ci-dessous.

$x_i$	$x_1$	$x_2$	$...$	$x_n$
$\mathbb{P}(X=x_i)$	$p_1$	$p_2$	$...$	$p_n$

On rappelle que :

$\displaystyle E(X)=\sum_{i=1}^n p_ix_i$
$\displaystyle V(X)=\sum_{i=1}^n p_i(x_i-E(X))^2$

Nous allons démontrer que $\displaystyle V(X)=E\left(X^2\right)-\left(E(X)\right)^2$

Expliquer pourquoi $\displaystyle E\left(X^2\right)=\sum_{i=1}^n p_ix_i^2$ .
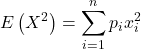
En partant de la formule $\displaystyle V(X)=\sum_{i=1}^n p_i(x_i-E(X))^2$ , démontrer que $\displaystyle V(X)=\left(\sum_{i=1}^n p_ix_i^2\right)-\sum_{i=1}^n 2E(X)p_ix_i+\sum_{i=1}^n p_i\left(E(X)\right)^2$ .
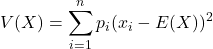
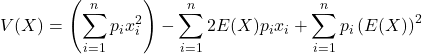
Factoriser les deuxième somme puis la troisième somme.
Conclure.

II. Etude d’une fonction

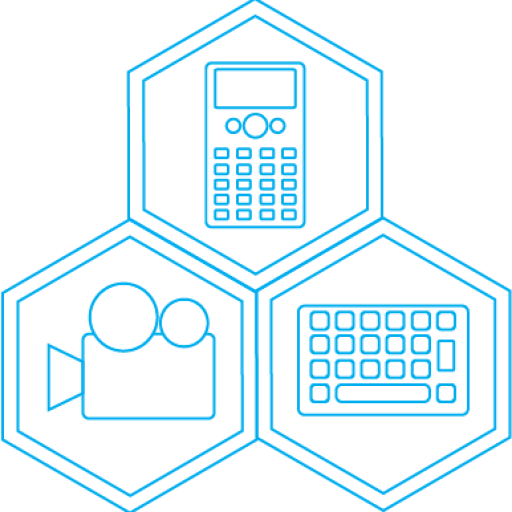
Soit $X$ une variable aléatoire.
Soit la fonction $f$ définie sur $\mathbb{R}$ par $f(x)=E\left((X-x)^2\right)$ .

Démontrer que $f(x)=x^2-2E(X)x+E\left(X^2\right)$ .
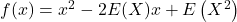
Quelle est la nature de la fonction $f$ ?
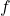
En déduire le sens de variation de la fonction $f$ .
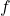
La fonction $f$ admet-elle un extremum? Si oui, quel est-il et pour quelle valeur de $x$ est-il atteint?
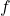
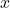
En déduire le signe de $f(x)$ selon les valeurs de $x$ .
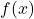
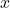
De quel signe est le discriminant du polynôme $f(x)$ ? Justifier.