Dans cette activité, nous allons estimer l’aire sous une parabole (partie I) puis le nombre \pi (partie II) par la méthode de Monté-Carlo.
Les deux parties sont totalement indépendants.
I – Aire sous la parabole
Nous allons proposer de calculer une estimation de l’aire délimitée par la parabole de la fonction carré, l’axe des abscisses et la droite d’équation ![]()
- Sous geogebra, tracer la courbe représentative de la fonction carrée, puis la droite d’équation
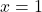
- Créer le carré (polygône) de côté 1 passant par les points de coordonnées
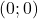
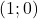
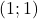
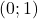
- Créer un curseur
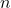
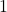
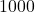
- Dans la ligne de saisie, écrire:
E=(random(),random())Où se place le point
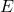 ?
? - Dans la ligne de saisie, écrire:
Liste_1=Séquence((random(),random()),i,1,n)Que se passe-t-il?
Faites varier le curseur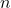 . Que se passe-t-il?
. Que se passe-t-il? - Nous allons créer la région sous la courbe.
- Donner un encadrement de
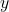
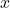
- Compléter la saisie suivante qui permet de créer la région sous la courbe.
Région= (...<= x <=...) && (...<= y <=...)
- Donner un encadrement de
- Que fait la saisie suivante?
Liste_2 = Séquence(EstDansRégion(Elément(Liste_1,i),Région),i,1,n) - En saisissant
S=Somme[Liste_2], on obtient le nombre de points sous la courbe.
Que saisir pour avoir la proportion de points sous la courbe parmi tous les points? Pour ce nombre, on choisira Propriété/Algèbre et on décochera Symbolique. - Faire varier
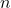
- Quelle est la probabilité qu’un point du carré soit sous la courbe?
- Estimer la valeur de l’aire sous la courbe?
On pourra supposer que la proportion de points sous la courbe parmi les points du carré est approximativement la même que la proportion d’aire sous la courbe par rapport à l’aire du carré
II – Estimation de 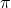
Nous allons proposer de calculer une estimation de l’aire d’un disque de rayon 1 unité.
- Tracer un cercle de rayon
1et de centre l’origine du repère. - Déterminer la valeur exacte de l’aire de ce disque.
- Tracer le carré de sommets les points de coordonnées
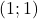
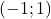
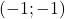
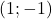
- Quelle est l’aire du carré?
- Créer un curseur
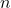
1à1000. - Soit
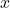
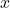
- Créer la région correspondant au disque.
- La commande
AléaUniforme(-1,1)retourne un nombre aléatoire compris entre-1et1.
Créer laListe_1des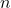
- Créer la
Liste_2qui indique si les points de la laListe_1sont dans le disque ou non. - Déterminer le nombre de points dans le disque.
- En déduire la proportion de points dans le disque parmi les points présents. Pour ce nombre, on choisira Propriété/Algèbre et on décochera Symbolique.
- Quelle est la probabilité qu’un point du carré soit dans le disque?
- Estimer la valeur du nombre